Origens
No ocidente, a sequência de Fibonacci apareceu pela primeira vez no livro Liber Abaci (1202) de Leonardo de Pisa, conhecido como Fibonacci, embora ela já tivesse sido descrita por matemáticos indianos. Fibonacci considerou o crescimento de uma população idealizada (não realista biologicamente) de coelhos. Os números descrevem o número de casais na população de coelhos depois de n meses se for suposto que:
- no primeiro mês nasce apenas um casal,
- casais amadurecem sexualmente (e reproduzem-se) apenas após o segundo mês de vida,
- não há problemas genéticos no cruzamento consanguíneo,
- todos os meses, cada casal fértil dá a luz a um novo casal, e
- os coelhos nunca morrem.
Mas genericamente, chama-se sequência de Fibonacci qualquer função g onde g(n + 2) = g(n) + g(n + 1). Essas funções são precisamente as de formato g(n) = aF(n) + bF(n + 1) para alguns números a e b, então as sequências de Fibonacci formam um espaço vetorial com as funções F(n) e F(n + 1) como base.
Em particular, a sequência de Fibonacci com F(1) = 1 e F(2) = 3 é conhecida como os números de Lucas. A importância dos números de Lucas L(n) reside no fato deles gerarem a Proporção áurea para as enésimas potências:
Os números de Lucas se relacionam com os de Fibonacci pela fórmula:
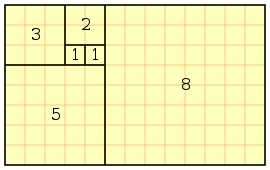
Com esta fórmula podemos montar a sequência de Fibonacci e descobrir, por exemplo, quantos coelhos foram gerados no sexto mês, basta aplicar a fórmula descrita acima até chegar ao ponto inicial de 1 e 1, como mostra a figura abaixo:

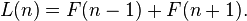




Nenhum comentário:
Postar um comentário